In diesem Monat gibt es einen TikZ-Adventskalender, bei dem jeden Tag eine Funktion bzw. ein Aspekt des Zeichenpaketes gezeigt wird. Allerdings soll dieser Blogeintrag keine vollständige Anleitung für TikZ werden – das wäre in diesem Format auch nicht möglich –, sondern wie die kleinen Schokoladenstückchen in anderen Adventskalendern den Geschmack anregen und Lust auf mehr machen.
Wer sich nach den Weihnachtsferien dann tiefer in das Paket einarbeiten will, dem sei die hervorragende und sehr umfangreiche Anleitung (pgfmanual.pdf) des Paketes empfohlen, die unter anderem verschiedene und gut verständliche Tutorials enthält.
Grundlagen
Bevor wir zum ersten Türchen kommen, müssen wir uns mit ein paar grundlegenden Konzepten von TikZ vertraut machen.
PGF und TikZ
PGF ist der eigentliche Kern des Paketes, auf dem alles andere aufbaut, weshalb die Dokumentation auch pgfmanual.pdf heißt. TikZ ist sozusagen die Schnittstelle zwischen dem Anwender und PGF. (Theoretisch sind auch weitere Schnittstellen denkbar.)
Zeichenumgebung und -befehl
Das Paket stellt die Umgebung {tikzpicture} sowie den Befehl \tikz zu Verfügung, wobei erstere für größere Abbildungen und letzterer bspw. für einzelne Inline-Zeichenbefehle geeignet ist. Beide haben ein optionales Argument, über das verschiedene Einstellungen vorgenommen werden können.
Verschachtelte Zeichnungen
Um Einstellungen nur für einen bestimmten Teil einer Abbildung vorzunehmen, verwendet man die Umgebung {scope}.
Pfad-Befehle
Jede TikZ-Zeichnung besteht aus der Angabe mindestens eines Pfades. Ein Pfad beginnt dabei mit einem der folgenden Befehle und endet mit einem Semikolon ;. Zwischen Befehl und Semikolon stehen verschiedene Zeicheninstruktionen und Optionen, die wir mit jedem Türchen nach und nach kennen lernen werden.
\pathist der Basis-Pfadbefehl, der ohne Weiteres nicht zu einer Ausgabe führt.\drawzeichnet den angegeben Pfad als Linie. Dieser Befehl ist eine Abkürzung für\path [draw].\fillzeichnet den angegeben Pfad als Fläche. Dieser Befehl ist eine Abkürzung für\path [fill].\filldrawzeichnet den angegeben Pfad als Linie und als Fläche. Dieser Befehl ist eine Abkürzung für\path [fill, draw].
Es gibt noch wesentlich mehr Pfad-Befehle, die wir zum Teil später noch benutzen werden. Eine komplette Liste findet sich in der TikZ-Anleitung in Abschnitt 15.1.
Alle folgenden Abschnittsnummern beziehen sich auf diese Anleitung; Paketversion 3.0.1a, Dezember 2015.
Optionen
Sowohl \tikz, {tikzpicture} und {scope} als auch die Pfadbefehle können eine ganze Reihe von Optionen verarbeiten, die jeweils in eckigen Klammern und durch Komma getrennt angegeben werden. Ungewöhnlich ist, dass die Namen der Optionen auch Leerzeichen enthalten können.
Bibliotheken
TikZ wird mit einer Reihe von ergänzenden Bibliotheken ausgeliefert, die bei Bedarf mit dem Befehl \usetikzlibrary geladen werden können. Die Bibliotheken sind in den Abschnitten V und VI dokumentiert.
Englische Begriffe / Übersetzung
Auch wenn ich eigentlich ein Freund davon bin, deutsche Begriffe anstelle von Anglizismen zu verwenden, habe ich mich entschieden, im Folgenden bei den englischen Bezeichnungen wie Node zu bleiben. Zum einen, weil diese Begriffe sich nicht ohne Weiteres sinnvoll übersetzen lassen und zum anderen, weil die Dokumentation auch auf Englisch ist und man dann meine individuellen Übersetzungen nicht als neue Vokabeln lernen muss.
Minimalbeispiel / Vorlage für die Türchen
Die Code-Abschnitte der Türchen ergeben dieses Mal nicht gemeinsam ein Beispiel, sondern stehen jeweils für sich und müssen in ein Minimaldokument wie das folgende eingefügt werden.
\documentclass[border=5mm,tikz]{standalone}
Als nächstes laden wir tikz und für einige der Türchen werden wir außerdem zusätzliche Funktionen über Bibliotheken laden müssen.
\usepackage{tikz} % \usetikzlibrary{...}
An dieser Stelle müssen später die jeweiligen Zeichenbefehle eingefügt werden.
\begin{document} \begin{tikzpicture} % Pfad-Befehle \end{tikzpicture} \end{document}
Türchen 1 – Gerade Linien
\begin{tikzpicture}Gerade Linien lassen sich einfach mit einem doppelten Divis -- erzeugen. Die Koordinaten geben wir als x-y-Paare an.
\draw (0,0) -- (0,2) -- (2,2);
Steht zwischen zwei Koordinaten keine Zeichen-Operation, entsteht eine Lücke im Pfad.
\draw (3,0) -- (5,0) (3,2) -- (5,2);
Neben -- kann auch to benutzt werden, wobei letzteres wesentlich flexibler ist, wie wir später sehen werden.
\draw (6,0) to (6,2) to (8,2);
Mit |- und -| ist es außerdem möglich, zwei Punkte nur mit vertikalen und horizontalen Linien zu verbinden.
\draw (9,0) -| (11,2); \draw (12,0) |- (14,2);
\end{tikzpicture}Türchen 2 – Koordinatensysteme
Kartesische Koordinaten in 2D werden wie bereits bekannt als x-y-Paare angegeben. Per Voreinstellung entspricht ein Wert von 1 einem Zentimeter.
\begin{tikzpicture} \draw (0,0) -- (1,0); \draw (2,0) -- (2,1); \draw (3,0) -- (4,0) -- (4,1) -- (3,1) -- cycle; \end{tikzpicture}
Die cycle-Operation schließt einen Pfad. Tipp: Vergleichen Sie einmal das Ergebnis, wenn Sie statt cycle die Koordinate (3,0) schreiben.
Kartesische Koordinaten in 3D werden als x-y-z-Paare angegeben, wobei x und y die Papierebene aufspannen und z aus dem Papier heraus zeigt. Die Einstellung der Basisvektoren lässt sich allerdings leicht ändern.
\begin{tikzpicture} \draw (0,0,0) -- (1,0,0); \draw (2,0,0) -- (2,1,0); \draw (3,0,0) -- (3,0,1); \draw (4,0,0) -| (5,1,0) -- (5,1,1) |- (4,0,1) -- cycle; \end{tikzpicture}
Polarkoordinaten werden als Paare aus φ und r, getrennt durch einen Doppelpunkt angegeben.
\begin{tikzpicture} \draw (0:0) -- (0:1) -- (45:1) -- (90:1) -- (135:1) -- (180:1) -- (225:1) -- (270:1) -- (-45:1) -- cycle; \end{tikzpicture}
Anstelle von r können auch zwei verschiedene Radien, getrennt durch and, angeben werden.
\begin{tikzpicture} \draw (0:0) -- (0:2 and 1) -- (45:2 and 1) -- (90:2 and 1) -- (135:2 and 1) -- (180:2 and 1) -- (225:2 and 1) -- (270:2 and 1) -- (-45:2 and 1) -- cycle; \end{tikzpicture}
Eine ausführliche Beschreibung inkl. weiterer Koordinatensysteme findet sich in Abschnitt 13.
Türchen 3 – Rechtecke, Gitter, Kreise, Ellipsen
\begin{tikzpicture}Rechtecke werden durch die Operation rectangle zwischen zwei Koordinaten erzeugt.
\fill (0,0) rectangle (2,2);
Gitter erzeugt man analog mit der grid-Operation. Die Gitterabstände können durch verschiedene Optionen geändert werden. Allerdings kann es vorkommen, dass durch Rundungsfehler das umliegende Rechteck nicht (vollständig) gezeichnet wird.
\draw (3,0) grid (5,2); \draw [step=0.5] (6,0) grid (8,2); \draw [xstep=0.25, ystep=0.5] (9,0) grid (11,2); \draw (11.75,-0.25) grid (14.25,2.25);
\end{tikzpicture}Kreise und Ellipsen werden mit circle bzw. ellipse erzeugt, wobei beide Operationen synonym sind.
\begin{tikzpicture} \fill (0,0) circle [radius=1]; \fill (3,0) ellipse [x radius = 1, y radius = 0.5]; \fill (6,0) ellipse [x radius = 1, y radius = 0.5, rotate = 35]; \draw (9,0) circle [x radius = 1, y radius = 0.5, rotate = 35]; \end{tikzpicture}
Türchen 4 – Linienstile I
Die Strichstärke kann man entweder durch Optionen wie thin oder thick (Abschnitt 15.3.1) oder mit line width festlegen.
\begin{tikzpicture} \draw (0,0) |- (2,2); \draw [thin] (3,0) |- (5,2); \draw [thick] (6,0) |- (8,2); \draw [line width = 2mm] (9,0) |- (11,2); \end{tikzpicture}
Eine Option, die der Umgebung übergeben wird, wirkt auf alle Pfade. Hier stellen wir ein, dass alle Linien dick sein sollen.
\begin{tikzpicture}[thick]Für gestrichelte Linien gibt es ebenfalls einfache Optionen wie dashed (Abschnitt 15.3.2) oder die Möglichkeit, ein Muster mittels dash pattern zu definieren.
\draw (0,0) |- (2,2); \draw [dashed] (3,0) |- (5,2); \draw [dotted] (6,0) |- (8,2); \draw [dash pattern = on 1mm off 2mm on 5mm off 1mm] (9,0) |- (11,2);
\end{tikzpicture}\begin{tikzpicture}[thick]Abgerundete Ecken kann man mit rounded corners einstellen. Gibt man dabei keinen Wert an, greift die Voreinstellung von 4 pt.
\draw (0,0) |- (2,2); \draw [rounded corners] (3,0) |- (5,2); \draw [rounded corners = 5mm] (6,0) |- (8,2);
Außerdem kann man den Anfang bzw. das Ende einer Linie verkürzen, was insbesondere bei gebogenen Linien praktisch sein kann.
\draw [shorten <=5mm, shorten >=10mm] (9,0) |- (11,2);
\end{tikzpicture}Die Art der Linienenden kann über die Option line cap eingestellt werden.
In diesem Beispiel verwenden wir {scope}s, um verschiedene Optionen auf Teile der Abbildung zu beschränken
\begin{tikzpicture} \begin{scope}[line width = 2mm] \draw (0,0) |- (2,2); \draw [line cap = butt] (6,0) |- (8,2); \draw [line cap = rect] (3,0) |- (5,2); \draw [line cap = round] (9,0) |- (11,2); \end{scope} \begin{scope}[thick, white] \draw (0,0) |- (2,2); \draw (3,0) |- (5,2); \draw (6,0) |- (8,2); \draw (9,0) |- (11,2); \end{scope} \end{tikzpicture}
Das Aussehen der Ecken kann über die Option line join festgelegt werden.
\begin{tikzpicture}[line width = 3mm] \draw (0,0) |- (2,2) -- cycle; \draw [line join = miter] (9,0) |- (11,2) -- cycle; \draw [line join = round] (6,0) |- (8,2) -- cycle; \draw [line join = bevel] (3,0) |- (5,2) -- cycle; \end{tikzpicture}
Doppelte Linien werden mit double erzeugt. Dabei kann als Wert eine Farbe für die innere Linie angeben werden. Der Abstand der äußeren Linien bzw. die Stärke der inneren wird mit double distance festgelegt.
\begin{tikzpicture}[thick] \draw (0,0) |- (2,2); \draw [double] (3,0) |- (5,2); \draw [red, double = black] (6,0) |- (8,2); \draw [line width = 1mm, double, double distance = 1mm] (9,0) |- (11,2); \end{tikzpicture}
Türchen 5 – Farbe und Transparenz
Jedem Pfadbefehl kann eine Farbe als Option angeben werden. Die Farben werden durch das Paket xcolor, das von tikz geladen wird, zur Verfügung gestellt (siehe auch das Beispiel des nächsten Monats). Damit ist es bei Bedarf auch möglich eigene Farben zu definieren.
Außerdem können über Optionen wie fill oder draw verschiedene Farben für einen Pfad definiert werden.
\begin{tikzpicture}[line width = 2mm] \draw [blue] (0,0) rectangle (2,2); \fill [blue] (3,0) rectangle (5,2); \filldraw [blue] (6,0) rectangle (8,2); \fill [draw = blue] (9,0) rectangle (10,1); \draw [fill = blue] (10,1) rectangle (11,2); \end{tikzpicture}
Außerdem besteht die Möglichkeiten verschiedene Farben zu mischen. Eine mit Ausrufezeichen an einen Farbnamen angehängte Zahl zwischen 0 und 100 gibt die „Farbmenge“ an. Folgt ein weiteres Ausrufezeichen und noch ein Farbname, werden beide Farben gemischt, wobei die Zahl den Anteil der ersten Farbe angibt.
\begin{tikzpicture} \fill [blue!80] (0,0) rectangle (2,2); \fill [blue!80!white] (3,0) rectangle (5,2); \fill [blue!30!black] (6,0) rectangle (8,2); \fill [blue!70!black] (9,0) rectangle (11,2); \end{tikzpicture}
Die Deckkraft bzw. die Transparenz einer Farbe kann über die Option opacity bzw. draw opacity und fill opacity angeben werden. Bei einem Wert von 1 ist eine Farbe komplett deckend und bei 0 unsichtbar.
Außerdem gibt es Optionen wie nearly transparent, semitransparent oder nearly opaque (Abschnitt 23.2)
\begin{tikzpicture} \fill (0.25,0.25) rectangle (2.25,2.25); \fill [blue] (0,0) rectangle (2,2); \fill (3.25,0.25) rectangle (5.25,2.25); \fill [blue!60] (3,0) rectangle (5,2); \fill (6.25,0.25) rectangle (8.25,2.25); \fill [blue, opacity = 0.6] (6,0) rectangle (8,2); \fill (9.25,0.25) rectangle (11.25,2.25); \filldraw [ draw = white, draw opacity = 0.5, fill = blue, fill opacity = 0.8, line width = 2mm ] (9,0) rectangle (11,2); \end{tikzpicture}
Da TikZ xcolor für die Farbigkeit verwendet, sei hier auch ausdrücklich auf dessen Dokumentation verwiesen.
Türchen 6 – Text (Nodes I)
\begin{tikzpicture}[thick]Um einer Abbildung Text hinzuzufügen, vewendet man in TikZ die sog. Nodes. Man kann sie entweder mitten auf einem Pfad mit der Operation node hinzufügen, dann werden Sie an der letzten Koordinate platziert, oder mit dem Befehl ode, dann kann die Position mit at bestimmt werden. In beiden Fällen wird der Inhalt in geschweiften Klammern angegeben.
\path (0,0) node {Nikolaus}; \node at (2,0) {Gabe};
Sofern nicht anders eingestellt, wird ein Node mittig auf eine Koordinate gesetzt. Mit Optionen wie above oder left kann die Position relativ zur Koordinate geändert werden (Abschnitt 17.5.2).
\draw (4,0) -- (5,1) node [above] {Rute}; \draw (7,2) -- (6,1) node [below right] {Stiefel};
Des Weiteren kann die Position durch die Optionen midway und pos auf zwei vorhergehende Koordinaten bezogen werden.
Der Hintergrund eines Nodes ist durchsichtig, sofern nicht mit fill gearbeitet wird.
\draw (8,0) -- (8,2) node [ midway, fill = white, ] {Schnee}; \draw (9,0) -- (9,2) node [ pos = 0.25, fill = white, ] {Apfel};
Sind die Koordinaten durch eine Ecke (|- oder -|) verbunden, beziehen sich Werte kleiner 0.5 auf das Stück vor der Ecke und Werte größer 0.5 auf das Stück danach. 0.5 liegt immer auf der Ecke, auch wenn die Schenkel verschieden lang sind!
Tipp: Probieren sie für pos auch Werte größer als Eins bzw. kleiner als Null.
\draw (10,0) |- (14,2) node [ pos = 0.25, fill = white, ] {Nuss} node [ pos = 0.75, below, ] {Schokolade} node [ pos = 0.5, above, ] {Mandarine};
\end{tikzpicture}\begin{tikzpicture} \node at (0,0) {Nikolaus};
Mit der Option font kann man die Schrift des Textes beeinflussen. Das ist insbesondere dann sinnvoller, als dies direkt im Text-Argument zu machen, wenn die Schrift Teil einer nutzerdefinierten Option bzw. eines Stils wird.
\node [font = \sffamily\bfseries] at (2,0) {Gabe};
Mehrzeiliger Text ist nur dann möglich, wenn mit align explizit eine Ausrichtung angeben wurde (Abschnitt 17.4.3). Zeilenumbrüche können dann mit \\ erzeugt werden; Absätze (Leerzeilen oder \par) werden dagegen ignoriert.
\node [align = left] at (4,0) { Lieber,\\ guter\\ Weihnachts-\\ mann }; \node [align = center] at (6,0) { schau\\ mich\\ nicht so\\ böse an, }; \node [align = right] at (8,0) { stecke\\ deine\\ Rute\\ ein, };
Wird einem Node dagegen mit text width explizit eine Textbreite angeben, wird der Text automatisch umbrochen und dann sind auch Absätze erlaubt (Abschnitt 17.4.3).
\node [text width = 18mm] at (10,0) { Will auch immer artig sein! Ehrlich! };
Mit den Optionen fill und draw kann der Umriss eines Nodes gezeichnet bzw. sein Hintergrund gefüllt werden. Wird eine Farbe als Option angeben, wirkt sie auf den Text, die Füllung und den Umriss, sofern nicht anders angeben. (Analog zu den Optionen fill und draw gibt es auch text, um explizit die Textfarbe zu wählen.)
Die Form eines Nodes kann durch Optionen wir circle geändert werden (Abschnitte 17.2 und 67).
\node [blue, draw, thick, circle] at (12,0) {Geschenk}; \node [blue, draw = black, fill = blue!20] at (14,0) {Stiefel};
\end{tikzpicture}Türchen 7 – Gebogene Linien I
\begin{tikzpicture}[ultra thick]
Bögen zeichnet man mit der arc-Operation, wobei man den Winkel auch mit nur einem Start- oder Endpunkt und delta angle angeben kann. Außerdem können wie bei circle zwei verschiedene Radien angeben werden.
\draw (0,0) arc [ start angle = 180, end angle = 90, radius = 2, ]; \draw [blue] (0:2) arc [ start angle = 0, end angle = 90, radius = 2, ];
Einfache Sinus- oder Kosinuskurven kann man mit den Operationen sin und cos erzeugen, wobei diese zwischen zwei Koordinaten jeweils nur ein Teilstück der Länge π/2 zeichnen. Für komplexere, beliebige Funktionen steht ggf. die plot-Operation zur Verfügung.
\draw (3,1) sin (4,2) cos (5,1) sin (6,0) cos (7,1) sin (8,2) cos (9,1) sin (10,0) cos (11,1); \draw [blue] (3,0) cos (3.5,1) sin (4,2) cos (4.5,1) sin (5,0) cos (5.5,1) sin (6,2) cos (6.5,1) sin (7,0) cos (7.5,1) sin (8,2) cos (8.5,1) sin (9,0) cos (9.5,1) sin (10,2) cos (10.5,1) sin (11,0);
Außerdem gibt es mit der Operation parabola eine einfache Möglichkeit, Parabeln zu zeichnen. Dabei kann mit bend (…) oder bend at end bzw. bend at end angeben werden, wo das Extremum liegt.
\draw (12,0) parabola (14,2); \draw [blue] (12,0) parabola bend (13,2) (14,0); \draw [purple] (12,0) parabola [bend at end] (14,2);
\end{tikzpicture}Türchen 8 – Gebogene Linien II
\begin{tikzpicture}[ultra thick]
Wie in Türchen 1 schon angekündigt, kann die to-Operation viel mehr als nur gerade Linien erzeugen: Bspw. mit bend left und bend right geschwungene Linien. Mit loosenes kann dabei der Schwung beeinflusst werden.
\draw (0,0) to[bend left] (2,2); \draw [blue] (0,0) to[bend right] (2,2); \draw [green!50!black] (0,0) to[bend right, looseness = 2] (2,2); \draw [purple] (0,0) to[bend left, looseness = 0.5] (2,2);
Neben den bend-Optionen ist es auch möglich, den Ein- und Austrittswinkel der Linie über in und out festzulegen. Gibt man dabei zusätzlich die Option relative an, wird der Winkel auf die Gerade zwischen den beiden Koordinaten bezogen.
\draw (3,0) to[out = 110, in = 260] (5,2); \draw [blue] (3,0) to[out = 110, in = 260, looseness = 2] (5,2); \draw [purple] (3,0) to[ out = 110, in = 260, looseness = 0.5, ] (5,2);
Darüber hinaus ist es auch Möglich über controls die Kontrollpunkte für Bézierkurven festzulegen. Dabei gibt die erste Angabe nach controls den Kontrollpunkt für den Start und die Angabe nach and den für den Endpunkt an. Lässt man and und die zweite Angabe weg, gilt der Kontrollpunkt für Start- und Endpunkt.
Durch ein vorangestelltes Plus + werden die Angaben relativ zum Start- bzw. Endpunkt gemessen und nicht zum Ursprung des Koordinatensystems.
\draw (6,0) .. controls (7,1.25) and (8,0.75) .. (10,2); \draw [blue] (6,0) .. controls +(80:2) and +(-75:2) .. (10,2);
\end{tikzpicture}Die Dekoration show path construction kann hilfreich sein, um die Konstruktion eines Pfades zu visualisieren (Abschnitt 48.3). Und Paul Gaborits Antwort auf die Frage How does one pick control points to control Bézier curves in TikZ? auf TeX.SX veranschaulicht in einer Animation den Einfluss, den die Kontrollpunkte auf den Kurvenverlauf nehmen.
Türchen 9 – Pfeilspitzen
Für die erweiterten Pfeilspitzenfunktionen laden wir in der Präambel (FAQ 1) arrows.meta.
\usetikzlibrary{arrows.meta}
\begin{tikzpicture}[ultra thick]
Um einer Linie eine Pfeilspitze hinzuzufügen, gibt man als Option einen Divis - (Trennstrich) zusammen mit Größer‑/Kleinerzeichen >/< an.
\draw [->] (0,0) -- (2,2); \draw [<-] (2,0) -- (0,2);
Über die Option > kann das Aussehen aller Pfeilspitzen geändert werden; die Option < gibt es nicht!
Wir verwenden hier ein {scope}, um die Änderung auf einen Teil der Grafik zu beschränken.
\begin{scope}[>=Latex] \draw [<->] (3,0) -- (5,2); \end{scope}
Man kann auch mehr als ein </> verwenden, um mehrfache Spitzen zu erzeugen. Ein Unterstrich _ erzeugt dabei einen Abstand zwischen den Spitzen und ein Punkt . unterbricht die Verbindung zur eigentlichen Linie.
\draw [<_<___>->>>.>>] (6,0) -- (8,2);
Neben < und > als Spitze am Divis -, die jeweils die Einstellung der Option > verwenden, kann man auch direkt den Namen eines Spitzen-Typs angeben. Außerdem ist es möglich, die Spitze durch die Angabe von Optionen zu verändern; wegen der eckigen Klammern für die Spitzen-Optionen muss die gesamte Spitzen-Definition dann in geschweiften Klammern stehen.
\draw [Stealth-Circle] (8,0) -- (6,2); \draw [Bar-Arc Barb] (9,0) -- (11,2); \draw [Diamond-{Rays[n=6,scale=2]}] (11,0) -- (9,2); \draw [Rectangle-{>[scale=1.25]>>[scale=0.75]}] (10,2) -- (10,0);
\end{tikzpicture}Die vollständige Dokumentation zu Pfeilspitzen findet sich in Abschnitt 16.
Türchen 10 – Linienstile II
Um Linien zu „dekorieren“, gibt es verschiedene Bibliotheken, die wir je nach Bedarf laden müssen. \usetikzlibrary kann auch genutzt werden, um mehrere Bibliotheken gleichzeitig zu laden. (Es ist ratsam, auch die letzte Bibliothek mit einem Komma zu versehen, damit man es nicht vergisst, wenn man später eine weitere Bibliothek ergänzt.)
\usetikzlibrary{ decorations.pathmorphing, decorations.pathreplacing, decorations.shapes, decorations.text, }
Neben der Linienstärke geben wir dieses Mal auch bend left für die ganze Zeichenumgebung an, wodurch alle to-Operationen eine links-gekrümmte Linie erzeugen, sofern wir das nicht lokal ändern.
\begin{tikzpicture}[bend left, thick]
Um eine Linie zu dekorieren, müssen wir mit der Option decoration den Stil angeben und mit decorate explizit aktivieren. decorate kann als Option, aber auch als Operation verwendet werden, wie wir gleich sehen.
\draw (0,0) to (1,2); \draw [decoration = zigzag, decorate] (1,0) to (2,2); \draw [decoration = snake, decorate] (2,0) to (3,2); \draw [decoration = random steps, decorate] (3,0) to (4,2); \draw [decoration = saw, decorate] (4,0) to (5,2); \draw [decoration = bumps, decorate] (5,0) to (6,2); \draw [decoration = border, decorate] (6,0) to (7,2); \draw [decoration = crosses, decorate] (7,0) to (8,2); \draw [decoration = triangles, decorate] (8,0) to (9,2);
Wir können eine Linie auch durch Text ersetzen. Dabei geben wir über decoration nicht nur den Stil text along path, sondern auch zwei weitere Optionen für die Dekoration an.
\draw [ decoration = { text along path, text = {Toller Text}, text align = fit to path, }, decorate] (9,0) to (10,2);
Nun wollen wir eine rote, fette Linie zeichnen, die mit einer blauen geschweiften Klammer versehen ist. Dafür geben wir dem \draw-Befehl zunächst die Optionen für Stärke und Farbe sowie für die Dekoration. Allerdings nutzen wir decorate nicht direkt als Option für \draw, sondern gemeinsam mit Farbe und Stärke für postaction (Abschnitt 15.10). TikZ zeichnet den Pfad dann erneut mit den geänderten Optionen.
Den Text für die Klammer platzieren wir mit der node-Operation 5 mm über der Mitte der (ursprünglichen) Linie. sloped bedeutet, dass der Text parallel zu der jeweiligen Tangente durch seinen Bezugspunkt auf dem Pfad ausgerichtet wird.
\draw [ ultra thick, red, decoration = { brace, amplitude = 2mm, raise = 2mm }, postaction = {draw, blue, thin, decorate}, ] (11.5,2) -- (11.5,0) node [blue, midway, sloped, above = 5mm] {Text};
Wie bereits angedeutet, können wir decorate auch als eine Art Operation auf dem Pfad benutzen, um nur einen Teil desselben zu dekorieren. Der zu dekorierende Teil folgt der Operation in geschweiften Klammern.
\draw [decoration = triangles] (13,0) -- (13,2) decorate { to (15,1.5) -- (15,0) } -| (14,1);
\end{tikzpicture}Türchen 11 – Verläufe und Schatten
Für Verläufe benötigen wir die shadings- und für Schatten die shadows-Bibliothek.
\usetikzlibrary{ shadings, shadows, }
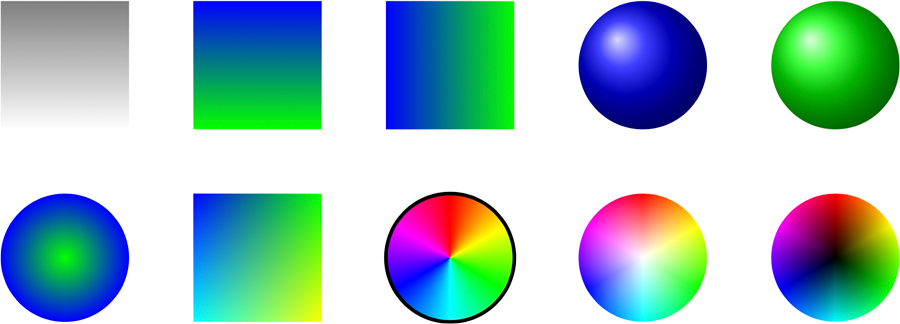
\begin{tikzpicture}Um einen Pfad mit einem Verlauf zu füllen, benutzt man entweder die Option shade oder abkürzend direkt den \shade-Befehl. Per Voreinstellung ist dies ein linearer Verlauf vertikal von grau nach weiß, wobei man die Farben durch Optionen verändern kann.
\path [shade] (0,0) rectangle (2,2); \shade [top color = blue, bottom color = green] (3,0) rectangle (5,2);
Gibt man statt einer oberen und unteren Farbe eine linke und eine rechte an, wird der Verlauf um 90° gedreht.
\shade [left color = blue, right color = green] (6,0) rectangle (8,2);
Eine andere Verlaufsart kann man der Option shading als Wert angeben, wie hier den Verlauf für eine 3D-Kugel, den man sinnvollerweise mit einer Kreisfläche kombiniert.
\shade [shading = ball] (10,1) circle [radius=1];
Wie bei der Richtung des linearen Verlaufs, kann man auch den Kugel-Verlauf implizit angeben, wenn man die Option ball color benutzt.
\shade [ball color = green] (13,1) circle [radius=1];
Einen radialen Verlauf erzeugt man implizit durch die Angabe einer inneren und einer äußeren Farbe.
\shade [inner color = green, outer color = blue] (1,-2) circle [radius = 1];
Die Angabe von vier Eckenfarben impliziert einen bilinear interpolierten Verlauf.
\shade [ upper left = blue, upper right = green, lower right = yellow, lower left = cyan, ] (3,-3) rectangle (5,-1);
Ein Farbrad-Verlauf muss explizit angeben werden, wobei drei Verschiedene Farben für die Mitte möglich sind.
Analog zu \filldraw kann mit \shadedraw der Pfad gleichzeitig als Linie gezeichnet werden.
\shadedraw [ultra thick, shading = color wheel] (7,-2) circle [radius = 1]; \shade [shading = color wheel white center] (10,-2) circle [radius = 1]; \shade [shading = color wheel black center] (13,-2) circle [radius = 1];
\end{tikzpicture}Die vollständige Dokumentation zu Verläufen findet sich in den Abschnitten 15.7 und 65.
Da Verläufe im Druck nicht ganz unproblematisch sind, sollte man in jedem Fall einen Testdruck machen (lassen) und sich ggf. mit der Druckerei abstimmen.
\begin{tikzpicture}Um eine Fläche mit einem Schlagschatten zu versehen, kann man die Option drop shadow verwenden.
\fill [blue, drop shadow] (0,0) rectangle (2,2);
Dabei kann man die Farbe des Schattens als Option zu drop shadow angeben. Allerdings hat der Schatten per Voreinstellung nur eine Deckkraft von 50 %, so dass man die Opazität bei Bedarf auch ändern muss (siehe Türchen 5).
\fill [blue, drop shadow = blue] (3,0) rectangle (5,2); \fill [blue, drop shadow = {green, opacity = 1}] (6,0) rectangle (8,2);
Außerdem kann man durch verschiedene Optionen die Größe und die Position des Schattens beeinflussen.
\fill [ blue, drop shadow = {% black, shadow scale = 1.1, shadow xshift = -0.25, shadow yshift = 0.125, }, ] (9,0) rectangle (11,2);
\begin{tikzpicture}In Abschnitt 66 werden alle Schatten-Funktionen beschrieben.
Türchen 12 – Nodes II und definierte Koordinaten
Für erweiterte Positionierungsoptionen für die Nodes laden wir die positioning-Bibliothek.
\usetikzlibrary{positioning}
Zu Beginn legen wir mit der Option outer sep = auto fest, dass TikZ versucht, automatisch die Linienstärke eines Nodes zu berücksichtigen, wenn andere Linien oder Elemente auf einen Node bezogen werden (Abschnitt 17.2.3).
\begin{tikzpicture}[outer sep = auto]
Als nächstes öffnen wir ein {scope} und definieren für dieses den Stil every node (Abschnitt 82.4.4), der auf alle Nodes wirkt, so dass diese einen dunkelgrünen Rahmen bekommen.
\begin{scope}[every node/.style = {draw = green!50!black}]
Darin platzieren wir einen Node, der keine Positionsangabe bekommt und damit auf (0,0) platziert wird. Wenn eine Angabe in runden Klammern ohne vorhergehendes at gemacht wird, erhält der Node einen Namen, über den man später darauf Bezug nehmen kann.
Wir legen also einen Node mit dem Inhalt X und dem Namen mein node an.
\node (mein node) {X};
Der nächste Node soll rechts von mein node liegen, den Namen M und den Inhalt M haben. Der Standard-Abstand kann über die Option node distance eingestellt werden.
\node (M) [right = of mein node] {M};
Nun platzieren wir noch zwei weitere Nodes, geben dieses Mal aber den Abstand explizit an.
\node (A) [right = 4mm of M] {A}; \node (S) [right = 4mm of A] {S};
\end{scope}
Die Node-Namen können wir auch verwenden, um Linien zwischen diesen zu zeichnen. Sofern wir dabei nur den Namen der Nodes angeben, wählt TikZ automatisch geeignete Punkte auf dem Umriss der Nodes für die Verbindungslinie. Alternativ dazu kann man den sog. Anker auch explizit angeben: zum einen durch Kompass-Angaben und zum anderen durch Winkelangaben, wobei letztere nur bei Kreisformen wirklich sinnvoll sind. Eine vollständige Liste aller Node-Formen und deren Anker findet sich in Abschnitt 67.
\draw [thick, shorten < = 3mm, shorten > = 3mm] (mein node) -- (M); \begin{scope}[red] \draw (M) to [bend left] (S); \draw (M) to [bend right] (S); \draw (M.north west) to [bend left] (S.north east); \draw (M.south west) to [bend right] (S.south west); \draw (M.north) to [bend left, looseness = 1.5] (S.north); \draw (M.south east) to [bend right] (S.south east); \draw (M.20) -- (A.200); \draw (M.-20) -- (A.160); \draw (A.20) -- (S.200); \draw (A.-20) -- (S.160); \end{scope}
Als nächstes legen wir ein {scope} an, in dem alle Nodes kleine, rote Punkte sind, um die verschiedenen Positionierungsoptionen aufzulisten.
\begin{scope}[ every node/.style = { circle, fill = red, inner sep = 0mm, minimum size = 1mm, }, ] \node [above = 1mm of mein node] {}; \node [above left = 1mm of mein node] {}; \node [above right = 1mm of mein node] {}; \node [left = 1mm of mein node] {}; \node [below = 1mm of mein node] {}; \node [below left = 1mm of mein node] {}; \node [below right = 1mm of mein node] {}; \node [right = 1mm of mein node] {}; \end{scope}
Normalerweise wird ein Node immer bezogen auf seine Mitte – den Anker center – positioniert …
\begin{scope}[ every node/.style = { fill = green, inner sep = 0mm, minimum size = 1mm, }, ] \node at (A.north west) {}; \node at (A.south west) {}; \node at (A.north east) {}; \node at (A.south east) {}; \end{scope}
… über die Option anchor kann man den Bezugspunkt aber verändern.
\begin{scope}[ every node/.style = { fill = red, inner sep = 0mm, minimum size = 1mm, }, ] \node [anchor = south east] at (M.north west) {}; \node [anchor = north east] at (M.south west) {}; \node [anchor = south west] at (S.north east) {}; \node [anchor = north west] at (S.south east) {}; \end{scope}
Die Option anchor kann auch mit den Positionierungsoptionen kombiniert werden, muss dann aber danach gemacht werden. Hier überschreiben wir jeweils für die beiden roten Quadrate den automatisch gewählten Anker (south/north für das obere/untere) mit center.
\begin{scope}[ every node/.style = { fill, inner sep = 0mm, minimum size = 1mm, }, ] \node [green, above = 0mm of A.85] {}; \node [red, above = 0mm of A.95, anchor = center] {}; \node [green, below = 0mm of A.265] {}; \node [red, below = 0mm of A.275, anchor = center] {}; \end{scope}
\end{tikzpicture}\begin{tikzpicture}[thick]Eine weitere praktische Funktion ist das Festlegen von benannten Koordinaten. Diese sind im Prinzip auch Nodes, haben aber nur einen einzigen Anker.
Um eine solche Koordinate zu definieren können wir zum einen den Befehl \coordinate analog zu \node benutzen.
\coordinate (A) at (0,0); \coordinate (B) at (6,0);
Die benannten Koordinaten können wir im Folgenden anstelle der bisher bekannten mathematischen Koordinaten verwenden.
\draw (A) to[bend left] (B);
Außerdem können wir auch die coordinate-Operation, analog zu node benutzen.
\draw (A) -- (2,0.5) coordinate (C); \draw (A) -| (C); \draw (B) -- (C) coordinate [midway] (D); \draw (B) -| (D);
\end{tikzpicture}Türchen 13 – Dinge wiederholen (\foreach)
Beim Zeichnen kommt es häufig vor, dass bestimmte Elemente mehrfach vorkommen. Um solche Wiederholungen nicht manuell machen zu müssen und den Code damit übersichtlich und besser wartbar zu halten, bietet TikZ die Funktion \foreach bzw. die Operation \foreach
Wie oben mit every node können wir über den Stil every circle einen Radius für alle circle-Operationen voreinstellen.
\begin{tikzpicture}[every circle/.style = {radius = 0.5mm}]
Zunächst wollen wir auf einige ungerade x-Werte einen schwarzen Punkt zeichnen.
\foreach \x in {1,3,5,7,9,11} \fill (\x,0) circle;
Als nächstes sollen auf den geraden Werten blaue Punkte plaziert werden. Besonders praktisch ist, das TikZ dazu in der Lage ist, Folgen automatisch fortzuführen, wenn man ... verwendet.
\foreach \x in {2,4,...,12} \fill [blue] (\x,0) circle;
Sollen innerhalb der \foreach-Schleife mehrere Befehle ausgeführt werden, müssen diese in geschweiften Klammern zusammengefasst werden.
Mithilfe der Option count, kann man einen Befehl angeben, der die Nummer der aktuellen Wiederholung der Schleife zählt. Wir nutzen dies hier für die x-Position der Buchstaben.
\foreach \buchstabe [count = \zaehler] in {A,...,L} { \draw [green, thick] (\zaehler,0) circle [radius = 1.5mm]; \node at (\zaehler,0.35) {\buchstabe}; }
Durch die Option evaluate ist es uns sogar möglich mit der Variable der Schleife Berechnungen durchzuführen, was wir hier nutzen, um die Funktion y = x0,4 abzubilden.
Außerdem speichern wir mit der remember-Option jeweils den Wert der vorhergehenden Wiederholung.
\foreach \x [ evaluate = \x as \y using \x^0.4, remember = \x as \lastx (initially 1), ] in {1,...,12} { \fill [blue] (\x,\y) coordinate (C-\x) circle; \draw [blue] (C-\lastx) to[bend left] (C-\x); \node [font = \tiny] at (\x,\y+0.5) {\y}; }
Sollen in einer Schleife mehrere Wertelisten durchlaufen werden, trennen wir die Variablen sowie die Wertepaare (genauer Wertetupel) mit einem Schrägstrich /.
\foreach \pos/\text in {2/Frohe,5/Weihnachten,8/Ihnen,10.5/allen!} \node [font=\bfseries\sffamily] at (\pos,3.75) {\text};
\end{tikzpicture}Die \foreach-Funktion ist in Abschnitt 83 dokumentiert.
Übrigens kann \foreach auch außerhalb der Zeichenumgebung verwendet werden, wobei die geschweiften Klammern für den zu wiederholenden Teil dann obligatorisch sind. Man könnte bspw. schreiben
Unser Alphabet besteht aus den Buchstaben \foreach \A in {A,...,X} {\A, }Y und Z.
Siehe bspw. Special treatment for last item in \foreach-list auf TeX.SX zu der Frage, warum man hier nicht einfach {A,...,Z} schreiben kann.
Türchen 14 – Koordinaten berechnen
Für das Rechnen mit Koordinaten laden wird die Bibliothek calc und für die Berechnung von Schnittpunkten die intersections-Bibliothek.
\usetikzlibrary{ calc, intersections, }
\begin{tikzpicture}[thick]Zunächst definieren wir zwei Koordinaten A und B.
\coordinate (A) at (0,0); \coordinate (B) at (8,3);
Nun wollen wir die Koordinaten ermitteln, die A und B zu einem Rechteck ergänzen. Eine Möglichkeit ist es, |- und -| innerhalb der Koordinatenangabe zu verwenden.
\coordinate (C) at (A |- B); \coordinate (D) at (A -| B); \draw (A) rectangle (B); \draw (A) -- (B); \draw (C) -- (D);
Als nächstes Suchen wir Punkte, die auf der Verbindungslinie zwischen zwei Koordinaten liegen. Wie beim Mischen von Farben können wir die Syntax mit Ausrufezeichen ! benutzen und den Streckenanteil angeben. Der Wert kann auch kleiner 0 oder größer 1 sein.
\coordinate (E) at ($(A)!0.5!(B)$); \coordinate (G) at ($(A)!0.75!(B)$); \coordinate (I) at ($(A)!1.25!(D)$); \draw [green] (A) -- (B); \draw [lime] (A) -- (I);
Über die !-Syntax ist es uns außerdem möglich die Projektion einer Koordinate auf die Strecke zwischen zwei anderen Koordinaten zu ermitteln. F ist die Projektion von E und H die Projektion von G auf die Strecke AD.
\coordinate (F) at ($(A)!(E)!(D)$); \coordinate (H) at ($(A)!(G)!(D)$); \draw [brown] (A) -- (E) -- (D) (E) -- (F); \draw [orange] (A) -- (G) -- (D) (G) -- (H);
Darüber hinaus können wir Koordinaten sogar als Vektoren benutzen und diese ganz einfach miteinander verrechnen.
\coordinate (J) at ($(G)+(F)$); \coordinate (K) at ($1.2*(G)-0.6*(F)$); \draw [purple] (G) -- (F) -- (J); \draw [red] (G) -- (F) -- (J);
Bei Streckenabschnitten und Projektionen ist es außerdem möglich, die zweite Koordinate gleichzeitig um den Ursprung zu drehen.
\coordinate (L) at ($(A)!1!30:(F)$); \coordinate (M) at ($(E)!0.5!160:(B)$); \draw [violet] (A) -- (F) -- (L); \draw [magenta] (E) -- (B) -- (M);
Eine weitere Möglichkeit, mit Koordinaten zu rechnen, bietet uns die let Operation: Damit können wir innerhalb des Pfades die x- und y-Werte eines Punktes verwenden und mit der Funktion veclen daraus sogar eine Länge berechnen.
\draw [teal] let \p1=(A), \p2=(B) in ($(A)+(0,-\y2)$) -- (0,\y1-\y2) -- (90:{veclen(\x2-\x1,\y2-\y1)});
Zuletzt nutzen wir eine \foreach-Schleife, um alle Koordinaten in der Abbildung mit einem Punkt und ihrem Namen zu versehen.
\foreach \K in {A,...,M} { \fill [blue] (\K) circle [radius = 2pt] node [above = 3pt, fill = white, inner sep=1pt] {\K}; }
\end{tikzpicture}Alle at-Angaben, die wir zur Definition der Koordinaten verwendet haben, hätten wir übrigens auch direkt zum Zeichnen verwenden können; so ist es nur etwas übersichtlicher gewesen.
Die calc-Bibliothek ist in Abschnitt 13.5 und die let-Operation in Abschnitt 14.15 beschrieben. Die vielen mathematischen Ausdrücke und Funktionen, die TikZ bzw. PGF zur Verfügung stellt, stehen in Abschnitt 89.2.
\begin{tikzpicture}[thick]Zunächst zeichnen wir drei geschwungene Pfade, denen wir mit der Option name path einen Namen geben.
\draw [name path = pfad 1] (0,0) .. controls +(0:8) and +(180:8) .. (10,3); \draw [name path = pfad 2] (0,2) to[bend left] (10,0); \draw [name path = pfad 3] (10,2) to[out = 170, in = 190, looseness=10] (10,1);
Nun können wir mit der Option name intersections und deren Option of zwei Pfade angeben, deren Schnittpunkt(e) berechnet werden sollen. Per Voreinstellung werden diese mit (intersection-n) benannt.
\draw [blue, name intersections = {of = pfad 1 and pfad 2}] (0,0) -- (intersection-1);
Ist ein Schnittpunkt einmal berechnet, steht er wie andere benannte Koordinaten für alle folgenden Zwecke zur Verfügung, sofern er nicht durch eine weitere Berechnung überschrieben wird.
\draw [cyan] (intersection-1) -- ($(0,0)!(intersection-1)!(1,0)$);
Um dieses Überschreiben zu verhindern, können wir der intersection-Option durch die Option by auch von uns gewünschte Namen angeben – hier „Schnittpunkt 1“ für den ersten und ein schlichtes „B“ für den zweiten. Diese geben wir dabei als kommagetrennte Liste an. Hier benutzen wir einen leeren Pfad, für die Berechnung und nutzen die Ergebnisse später für zwei \node-Befehle.
\path [ name intersections = {% of = pfad 2 and pfad 3, by = {Schnittpunkt 1, B}, }, ] ; \node [ circle, fill = green, font = \scriptsize, inner sep = 1pt, ] at (Schnittpunkt 1) {A}; \node [ circle, fill = green, font = \scriptsize, inner sep = 1pt, ] at (B) {B};
\end{tikzpicture}Die intersections-Bibliothek ist in Abschnitt 13.3.2 dokumentiert.
Türchen 15 – Pics: Teilabbildungen wiederverwenden
Wir haben im 13. Türchen bereits gesehen, dass man Dinge mit \foreach wiederholen kann. Eine weitere praktische Funktion zur Vermeidung von redundantem Code sind die Pics: in sich geschlossene Teilabbilungen.
Eine vergleichbare aber nicht ganz so flexible Funktion bietet Adobe Illustrator mit den Symbolen.
\begin{tikzpicture}[Um ein Pic zu definieren, müssen wir innerhalb der Optionen von {tikzpicture} (oder \tikzset oder {scope}) den gewünschten Namen gefolgt von /.pic angeben.
stiefel/.pic = {
Innerhalb der Definition des Pics können wir alle Zeichenbefehle und Operationen verwenden. In diesem Fall zeichnen wir eine rot gefüllte Stiefelform mit einem weißen Besatz am Schaft.
\fill [red] (0,0) -- (0.2,0) -- (0.2,-0.6) arc [start angle = 0, delta angle = -90, radius = 0.15] to [out = 180, in = 0] (-0.1,-0.7) to [out = 180, in = 0] (-0.3,-0.75) arc [start angle = 270, delta angle = -180, radius = 0.15] to [out = 0, in = 180] (-0.15,-0.475) arc [start angle = 270, delta angle = 90, radius = 0.05] |- cycle; \fill [white, draw = gray, thin, rounded corners = 1pt] (-0.15,-0.1) rectangle (0.25,0.05); }
Ende des pic
}
Ende der Optionen von {tikzpicture}
]
Diese Stiefel wollen wir nun an einer dicken grünen, leicht durchhängenden Schnur aufhängen, die wir als Beziérkurve zeichnen.
\draw [ultra thick, green!70!black] (0,0) .. controls +(-35:2) and +(215:2) .. (8,0)
Die Stiefel selbst fügen wir noch innerhalb des mit \draw begonnenen Pfades mit einer foreach-Operation hinzu, um neun Stiefel gleichmäßig zu platzieren. Das Pic wird dann mit der Operation pic gefolgt von Optionen und dem Namen hinzugefügt. Die Positionierung orientiert sich an dem Ursprung, der in der Definition galt und hier etwa mittig im Besatz liegt.
Da die Pics ähnlich zu den Nodes sind, verstehen sie auch die meisten Optionen dieser. Hier verwenden wir pos für die Platzierung auf dem Pfad und sloped, um das Pic an die Pfadkrümmung „anzuschmiegen“.
foreach \p in {0.1,0.2,...,0.9} { pic [pos = \p, sloped] {stiefel} };
\end{tikzpicture}\begin{tikzpicture}[Nun wollen wir ausgehend vom ersten Beispiel das Stiefel-Pic so erweitern, dass wir jeden Stiefel individuell mit einem Buchstaben versehen können. Dazu müssen wir in der Definition einfach #1 verwenden; TikZ erkennt dann, dass das Pic einen Wert haben soll, den wir beim Benutzen mit angeben müssen (vgl. Abschnitt 82.4.4 sowie FAQ 10).
stiefel mit buchstabe/.pic = { \fill [red] (0,0) -- (0.2,0) -- (0.2,-0.6) arc [start angle = 0, delta angle = -90, radius = 0.15] to [out = 180, in = 0] (-0.1,-0.7) to [out = 180, in = 0] (-0.3,-0.75) arc [start angle = 270, delta angle = -180, radius = 0.15] to [out = 0, in = 180] (-0.15,-0.475) arc [start angle = 270, delta angle = 90, radius = 0.05] |- cycle; \fill [white, draw = gray, thin, rounded corners = 1pt] (-0.15,-0.1) rectangle (0.25,0.05); \node at (0.15,-0.15) [ circle, fill = green!70!black, text=white, draw = brown!70!black, thick, inner sep = 1pt, font = \itshape\bfseries\tiny, ] {#1}; }
Ende der Optionen von {tikzpicture}
]
Die Stiefel „hängen“ wir wie zuvor an eine grüne Schnur, nur dass wir nun eine foreach-Schleife mit zwei Variablen benutzen und den Buchstaben durch ein Gleichheitszeichen = als Wert an das Pic weitergeben, er ersetzt #1 aus der Definition. Außerdem verwenden wir die Funktion rand, die eine (pseudo-)zufällige Zahl zwischen –1 und 1 liefert (Abschnitt 89.3.6), um die Abstände etwas ungleichmäßiger zu machen.
\draw [ultra thick, green!70!black] (0,0) .. controls +(-35:2) and +(215:2) .. (8,0) foreach \p/\B in {% 0.1/M,0.2/E,0.3/R,0.4/R,0.5/Y, 0.6/X,0.7/M,0.8/A,0.9/S% } { pic [pos = \p+0.01*rand, sloped] {stiefel mit buchstabe = \B} };
\end{tikzpicture}Die Pics sind in Abschnitt 18 erklärt.
Türchen 16 – Beschneiden und Ausblenden
Zum „weichen” Ausblenden von Abbildungen oder Teilen davon müssen wir die fadings-Bibliothek laden.
\usetikzlibrary{fadings}
\begin{tikzpicture}Als erstes zeichnen wir ein Muster aus großen schwarzen Kreisen.
\foreach \n in {0,...,6} \draw (\n,0) [thick] circle [radius = 0.8] ;
Anschließend legen wir mit dem \clip-Befehl den Beschnittpfad fest, der für alle folgenden Abbildungsteile bzw. bis zum Ende des aktuellen {scope} gilt.
\clip (0,-0.5) rectangle (6,0.5);
Zuletzt zeichnen wir ein Muster aus blauen Kreisen, das nur innerhalb des zuvor definierten Bereichs sichtbar ist.
\foreach \n in {0,...,24} \draw [blue] (\n/4,0.4) circle [radius = 0.25] (\n/4,0) circle [radius = 0.25] (\n/4,-0.4) circle [radius = 0.25] ;
\end{tikzpicture}Anstelle von \clip kann man analog zu den anderen Pfad-Befehlen auch \path [clip] benutzen. Außerdem ist es möglich, den Beschnittpfad gleichzeitig auch zu zeichnen oder zu füllen. Dokumentiert ist diese Funktion in Abschnitt 15.9.
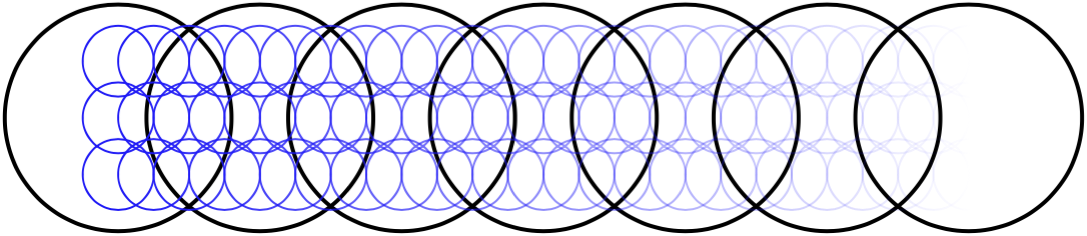
\begin{tikzpicture}Wie eben zeichnen wir zunächst das Muster aus schwarzen Kreisen.
\foreach \n in {0,...,6} \draw (\n,0) [thick] circle [radius = 0.8] ;
Anstelle von \clip nutzen wir dieses Mal \path mit der Option scope fading = east, um das folgende blaue Muster nach rechts auszublenden.
\path [scope fading = east] (0,-0.5) rectangle (6,0.5);
Auch hier folgt nun nur noch das blaue Kreismuster.
\foreach \n in {0,...,24} \draw [blue] (\n/4,0.4) circle [radius = 0.25] (\n/4,0) circle [radius = 0.25] (\n/4,-0.4) circle [radius = 0.25] ;
\end{tikzpicture}Statt die vorgefertigten Möglichkeiten für scope fading zu nutzen ist es auch möglich eigene Deckkraftmasken zu definieren. Die Anleitung dazu findet sich in Abschnitt 15.9.
Türchen 17 – Transformieren
\begin{tikzpicture}Als erstes wollen wir zwei Rechtecke rotieren und verwenden dazu die Option rotate. Wir stellen fest, dass die Drehung immer um (0,0) erfolgt.
\fill (0,0) rectangle (2,2); \fill [blue, semitransparent, rotate = 30] (0,0) rectangle (2,2); \fill [green, semitransparent, rotate = 25] (1,1) rectangle (2,2);
Wollen wir um einen anderen Punkt drehen, müssen wir die Option rotate around verwenden.
\fill (3,0) rectangle (5,2); \fill [blue, semitransparent, rotate around = {45:(4,1)}] (3,0) rectangle (5,2);
Als nächstes wollen wir ein Rechteck skalieren. Damit die Transformation auf seinen Mittelpunkt bezogen wird, verwenden wir statt scale scale around.
\fill (6,0) rectangle (8,2); \fill [blue, semitransparent, scale around = {1.1:(7,1)}] (6,0) rectangle (8,2);
Mit den Optionen xshift und yshift können wir ein Objekt verschieben, müssen dabei allerdings Werte mit Einheiten angeben.
\fill (9,0) rectangle (11,2); \fill [blue, semitransparent, xshift = 1mm, yshift = 2mm] (9,0) rectangle (11,2);
Um die Verschiebung in Einheiten des Koordinatensystems ausdrücken zu können, müssen wir shift benutzen und eine Koordinate angeben.
\fill (12,0) rectangle (14,2); \fill [blue, semitransparent, shift = {(0.2,-0.3)}] (12,0) rectangle (14,2);
\end{tikzpicture}Übrigens können alle Transformationen auch als Option zu {tikzpicture} oder {scope} angeben werden, um eine ganze Abbildung bzw. Teile davon gleichzeitig zu transformieren.
Hinweis für alle, die keine Angst vor Matrizen haben: Mit der Option cm ist es auch möglich eine eigene Transformationsmatrix zu definieren, die dann auf alle Koordinaten (Vektoren) angewandt wird. Beschrieben ist das wie alle anderen Transformationen in Abschnitt 25.3.
Türchen 18 – Relative Koordinaten
Eine weitere praktische Funktion von TikZ ist, dass wir neben
absoluten und benannten Koordinaten auch relative Koordinaten
verwenden können.
\begin{tikzpicture}Als erstes zeichnen wir ein Quadrat wie wir es bereits kennen mit absoluten Koordinaten.
\draw (0,0) -- (2,0) -- (2,2) -- (0,2) -- cycle;
Wenn wir das Quadrat aber nicht im Ursprung beginnen wollen, müssen wir etwas rechnen, um die anderen Ecken zu bestimmen. Dank der +-Syntax können wir diese Rechnung von TikZ übernehmen lassen: Eine Koordinate mit vorangestelltem + bezieht sich immer auf die letzte absolute Koordinate – (3,0) in diesem Fall.
\draw (3,0) -- +(2,0) -- +(2,2) -- +(0,2) -- cycle;
Anstelle von + können wir auch ++ benutzen. In diesem Fall wird auch der Bezugspunkt für folgende Koordinaten auf die neu berechnete geändert.
\draw (6,0) -- ++(2,0) -- ++(0,2) -- ++(-2,0) -- cycle;
Um den Unterschied zwischen + und ++ besser zu verstehen, zeichnen wir nun zunächst eine beliebige Form mit einer dicken schwarzen Linie und anschließend die manuelle Umrechnung auf absolute Koordinaten gestrichelt in weiß.
\draw [line width=2mm] (9,0) -- +(1,0) -- +(1,1) -- ++(2,1) -- +(0,1) -- (9,2) -- +(0,-0.5) -- ++(0.5,-0.5) -- (9.5,0.5); \draw [dashed, white] (9,0) -- (10,0) -- (10,1) -- (11,1) -- (11,2) -- (9,2) -- (9,1.5) -- (9.5,1.5) -- (9.5,0.5);
\end{tikzpicture}\begin{tikzpicture}Es ist auch möglich, eine Transformation auf eine einzelne Koordinate anzuwenden, indem wir sie in eckigen Klammern vor den ersten Wert schreiben. Die Option turn bedeutet, dass das Koordinatensystem für die einzelne betroffene Koordinate so transformiert wird, dass der Ursprung auf dieser Koordinate liegt und die x-Achse in Richtung der Tangente des Pfades in dem Punkt zeigt.
\draw [ultra thick] (0,0) to[out=45, in=200] ([scale=2]2,2) -- ([turn]250:4) -- ([turn]225:{sqrt(4^2+4^2)}) -- ++(0,-2);
Um das besser zu verstehen, wollen wir die Zeichnung nun wiederholen und dabei die on-the-fly transformierten Koordinatensysteme mit einzeichnen.
Die wiederholte Abbildung verpacken wir in ein {scope}, um sie nach rechts zu verschieben.
\begin{scope}[xshift = 70mm]
Zunächst wiederholen wir die Zeichnung selbst.
\draw [ultra thick, gray] (0,0) to[out=45, in=200] ([scale=2]2,2) -- ([turn]250:4) -- ([turn]225:{sqrt(4^2+4^2)}) -- ++(0,-2);
Dann zeichnen wir das untransformierte, der ganzen Zeichnung (genauer natürlich dem verschobenen {scope}[xshift = 70mm]) zugrunde liegende Koordinatensystem.
\begin{scope}[red, thin, ->] \draw (-1,0) -- (6,0) node [below] {$x = x_{(0,0)}$}; \draw (0,-1) -- (0,5) node [right] {$y = y_{(0,0)}$}; \end{scope}
Nun zeichnen wir das Koordinatensystem, das für die Koordinate ([turn]250:4) gilt, in blau, indem wir auf ein {scope} genau die Transformationen anwenden, die TikZ aufgrund von turn im Hintergrund auch ausführt.
\begin{scope}[blue, shift = {(4,4)}, rotate = 20] \draw [->] (-1,0) -- (1,0) node [above] {$x_{(4,4)}$}; \draw [->] (0,-1) -- (0,1) node [left] {$y_{(4,4)}$}; \draw [ultra thick] (0,0) -- (250:4); \end{scope}
Zuletzt zeichnen wir analog dazu noch das Koordinatensystem für ([turn]225:{sqrt(4^2+4^2)}) in rot.
\begin{scope}[teal, shift = {(4,0)}, rotate = 270] \draw [->] (-1,0) -- (1,0) node [left] {$x_{(4,0)}$}; \draw [->] (0,-1) -- (0,1) node [above] {$y_{(4,0)}$}; \draw [ultra thick] (0,0) -- (225:{sqrt(4^2+4^2)}); \end{scope}
Ende von {scope}[xshift = 70mm]
\end{scope}
\end{tikzpicture}Relative Koordinaten und turn werden in Abschnitt 13.4 beschrieben.
Türchen 19 – Edges
Die edge-Operation ist vergleichbar mit der to-Operation. Sie dient ebenfalls dazu, einer Zeichnung Linien hinzuzufügen, diese Linien sind aber im Gegensatz zu mit to erzeugten Linien nicht Teil des Pfades, auf dem die Operation edge ausgeführt wird, sondern werden separat zur Zeichnung hinzugefügt. Das erlaubt uns, jeder dieser Linien über Optionen ein eigenes Aussehen zu geben.
Wir laden die quotes-Bibliothek für eine Kurzschreibweise mit ", die wir später verwenden wollen.
\usetikzlibrary{quotes}
\begin{tikzpicture}[thin]Wir zeichnen zunächst einen Pfad von (0,0) über (2,2) zu (1,2). Mit der edge-Operation fügen wir diesem nun weitere Linien hinzu, dabei folgen auf die Operation ggf. Optionen und dann eine Koordinate. Die Startkoordinate ist die jeweils zuletzt gültige; bspw. (0,0) für die ersten beiden Edges.
\draw (0,0) edge [blue, bend left] (2,2) edge [green, dashed, bend right] (2,1) -- (2,2) -- (1,2) edge [teal] (1,1);
Jetzt platzieren wir vier Nodes, die wir gleich mit Edges verbinden wollen.
\node (A) at (3,0) {A}; \node (B) at (5,0) {B}; \node (C) at (5,2) {C}; \node (D) at (3,2) {D};
Dazu benutzen wir einen leeren Pfad. Per Option legen wir fest, dass alle Edges, die zu diesem Pfad gehören gestrichelt und mit Pfeilspitze sein sollen; auch dass sie überhaupt gezeichnet werden, müssen wir hier mit draw explizit angeben. Die Startkoordinate für alle drei Edges ist der Node (A).
\path [every edge/.style = {draw, dashed, ->}] (A) edge (B) edge (C) edge (D);
Das Platzieren von Nodes und das Zeichnen von Edges können wir auch mit nur einem einzigen Pfad-Befehl erledigen. Wir verwenden relative Koordinaten, um die Nodes alle auf den Punkt (6,0) zu beziehen, und die Namen der Nodes für die Edges.
\path [ every node/.style = {circle, fill = gray}, every edge/.style = {draw, ->}, ] (6,0) +(0:0) node (1) {1} +(15:2) node (2) {2} +(45:2) node (3) {3} +(75:2) node (4) {4} (1) edge (2) edge (3) edge (4);
Wir platzieren erneut vier Nodes.
\node (I) at (9,0) {I}; \node (II) at (11,0) {II}; \node (III) at (11,2) {III}; \node (IV) at (9,2) {IV};
Zuletzt verbinden wir auch diese mit Edges. Dazu legen wir in den Pfad-Optionen zunächst die Stile every edge und every edge quotes fest. Letzterer bezieht sich auf einen Node, der automatisch erstellt wird, wenn wir den gewünschten Inhalt in den Edge-Optionen in Anführungszeichen " notieren. Weitere Optionen für den Edge geben wir wie gewohnt durch Komma getrennt an und Optionen für den Node schreiben wir unmittelbar hinter das schließende Anführungszeichen (bei mehreren in geschweifte Klammen).
\path [ every edge/.style = {draw, <<-}, every edge quotes/.style = {circle, fill = white}, ] (I) edge ["a"] (II) edge ["b", blue] (III) edge ["c" text = black, blue] (IV) (II) edge ["d" {text = black, fill = red}, dashed, -] (III);
\end{tikzpicture}Edges sind in Abschnitt 17.12 und die quotes-Bibliothek in Abschnitt 17.10.4 beschrieben.
Es sei noch angemerkt, dass " kein richtiges Anführungszeichen ist! Im Deutschen benutzt man entweder „diese“ oder »diese«. Siehe dazu beispielsweise Typefacts: Anführungszeichen.
Türchen 20 – Labels und Pins (Nodes III)
Wie gestern laden wird die quotes-Bibliothek für die Kurzschreibweise mit ".
\usetikzlibrary{quotes}
\begin{tikzpicture}[ thick,
Über den Stil every label legen wir fest, dass alle Labels blau sein sollen, und mit label distance stellen wir den Abstand zwischen Node und Label ein.
every label/.style = {blue}, label distance = 2mm,
Mit den Stilen every pin und every pin edge legen wir das Aussehen der Pins bzw. der Verbindung zwischen Node und Pin fest. Außerdem legen wir mit pin distance den Abstand zwischen Node und Pin fest.
every pin/.style = {draw = teal, fill = black!20,}, every pin edge/.style = {draw, <-}, pin distance = 7mm,
Ende der Optionen für {tikzpicture}
]
Wir platzieren einen Node und fügen diesem mit der Option label verschiedene Labels hinzu. Dabei können wir die Position des Labels durch die Angabe eines Winkels, einer Platzierungs-Option oder eines Ankers festlegen. In eckigen Klammern können wir außerdem Optionen für das Label angeben.
\node at (0,0) [ draw, circle, label = {L1}, label = {[red]15:L2}, label = {below left:L3}, label = {south:L4}, ] {N1};
Analog zu den Labels können wir mit der Option pin einen Pin hinzufügen, der mit dem Node durch ein Edge verbunden wird.
\node at (4,0) [ draw, circle, pin = {P1}, pin = {[pin edge={orange, ->}, draw = red]15:P2}, pin = {below left:P3}, pin = {south:P4}, ] {N2};
Dank der quotes-Bibliothek können wir auch hier die "-Kurzschreibweise verwenden, wobei wir über die Optionen quotes mean label und quotes mean pin bestimmen können, ob diese Schreibweise für Labels oder Pins benutzt werden soll (Abschnitt 17.10.4).
\node at (8,0) ["Q"] {N3};
\end{tikzpicture}Labels und Pins werden in Abschnitt 17.10 erklärt.
Türchen 21 – Ebenen
Die einfachste Möglichkeit, mit (zwei) Ebenen zu arbeiten, ist die backgrounds-Bibliothek.
\usetikzlibrary{backgrounds}
\begin{tikzpicture}Wir zeichnen zunächst einen grün gefüllten Node, den wir mit W1 benennen.
\node [ fill = green!50!black, text = white, font = \sffamily\bfseries, align = center, inner sep = 3mm, draw = white, line width = 1mm, rounded corners, ] (W1) {Frohe\\Weihnachten!};
Anschließend fügen wir einige rote Kreise hinzu, die den Node allerdings überlagern. Wir können die Kreise leider nicht vorher zeichnen, weil die W1.x-Koordinaten nicht früher verfügbar sind.
\foreach \anchor in {north, north east, south east, south, south west, north west} \fill [red] (W1.\anchor) circle [radius = 0.25];
Wir zeichnen den Node erneut, allerdings an einer anderen Position und mit dem Namen W2.
\node at (5,0) [ fill = green!50!black, text = white, font = \sffamily\bfseries, align = center, inner sep = 3mm, draw = white, line width = 1mm, rounded corners, ] (W2) {Frohe\\Weihnachten!};
Und auch die Kreise zeichnen wir erneut. Nun aber in einem {scope} mit der Option on background layer, wodurch die Kreise auf eine Ebene hinter dem Node erscheinen.
\begin{scope}[on background layer] \foreach \anchor in {north, north east, south east, south, south west, north west} \fill [red] (W2.\anchor) circle [radius = 0.25]; \end{scope}
\end{tikzpicture}Die Bibliothek ermöglicht es uns außerdem die Zeichnung mit einem Untergrund zu versehen: Mit dem Stil background rectangle können wir einen Rahmen oder eine Fläche hinzufügen, wobei wir diese durch die Option show background rectangle zusätzlich aktivieren müssen. Analog dazu können wir mit background grid das Aussehen eines mit show background grid zu aktivierenden Gitters beeinflussen.
\begin{tikzpicture}[ background rectangle/.style = { fill = black!15, rounded corners, }, show background rectangle, background grid/.style = { draw = white, thick, }, show background grid, ]
Mit verschachtelten \foreach-Schleifen zeichnen wir einige blaue Kreise, deren Position durch die Verwendung von rand etwas zufällig wird.
\foreach \x in {0,...,7} { \foreach \y in {0,...,3} { \foreach \r in {0.1,0.275,0.4} \draw [thick, blue] (\x+rand*0.05,\y+rand*0.05) circle [radius = \r] ; } }
\end{tikzpicture}Generell hätten wir im letzten Beispiel das Gitter und die graue Fläche natürlich auch von Hand zeichnen können, die Verwendung der Bibliothek hat aber zwei entscheidende Vorteile: 1. wird die benötigte Größe automatisch an die Abbildung angepasst und 2. können wir diese Optionen auch global verwenden und damit allen Abbildung einen einheitlichen Hintergrund geben.
Die backgrounds-Bibliothek ist in Abschnitt 43 dokumentiert. Wer mehr als zwei Ebenen benötigt, kann diese selbst definieren, siehe dazu Abschnitt 108.
Türchen 22 – Quer über die Seite zeichnen
Eine weitere sehr nützliche Funktion von TikZ ist, dass man bei Bedarf eine Zeichnung auch über die aktuelle Seite legen kann, ohne dass die Zeichnung die Position der anderen Texte beeinflusst. Um das zu demonstrieren, verwenden wir heute nicht die standalone-Klasse und betrachten dieses Mal auch ein vollständiges Beispiel.
Als erstes laden wir die Klasse und legen ein eher kleines, quadratisches Papierformat fest.
\documentclass[paper=150mm:150mm]{scrartcl}
\usepackage{tikz} \usetikzlibrary{calc}
Nun definieren wir uns einen Befehl \mn (FAQ 10). Dieser erzeugt ein TikZ-Bild, das nur einen benannten Node enthält. Um auch außerhalb des Bildes auf den Namen zugreifen zu können, nutzen wir remember picture und mit baseline = (#1.base) sorgen wir dafür, dass die Zeichnung an der Grundlinie der Textzeile ausgerichtet wird.
\newcommand{\mn}[2]{% \tikz [remember picture, baseline = (#1.base)] \node [inner sep = 0pt, outer sep = 2mm] (#1) {$\displaystyle#2$}; }
Durch Änderung der Länge \jot bewirken wir einen größeren Abstand zwischen den Zeilen von {align} (FAQ 13).
\setlength{\jot}{25pt}
Außerdem blenden wir die Seitenzahlen aus.
\pagestyle{empty}
\begin{document}Zunächst schreiben wir eine mehrzeilige Formel mit {align}, wobei wir \mn für einige Terme verwenden: Im ersten Argument geben wir einen Node-Namen an und im zweiten den eigentlichen Term. Die Ausgabe unterscheidet sich praktisch kaum von demselben Code ohne \mn.
\begin{align} (\sin\alpha + \cos\alpha)^2 &= (\mn{s1}{\sin\alpha} + \mn{c1}{\cos\alpha}) \cdot (\mn{s2}{\sin\alpha} + \mn{c2}{\cos\alpha}) \\ &= \mn{sq}{\sin^2\alpha} + \sin\alpha\cos\alpha + \cos\alpha\sin\alpha + \mn{cq}{\cos^2\alpha} \\ &= 1 + \mn{2sc}{2\sin\alpha\cos\alpha} \\ &= 1 + \mn{f}{\frac{\sin(2\alpha)}{2}} \end{align}
Nun wollen wir diese Formel mit Pfeilen und Anmerkungen versehen: Um in diesem Bild auf die Namen der Nodes zugreifen zu können, benutzen wir auch hier remember picture und mit overlay legen wir fest, dass die Zeichnung selbst keinen Platz in Anspruch nimmt.
Für die Pfeile und Anmerkungen benutzen wir Nodes und Edges.
\begin{tikzpicture}[remember picture, overlay, thick, blue] \draw [every edge/.style = {draw, ->}] (s1.north) edge [bend left] (s2.north) edge [bend left] (c2.north) (c1.south) edge [bend right] (s2.south) edge [bend right] (c2.south); \draw (sq.south) -- ++(0,-0.3) -| (cq.south) node [pos = 0.25, fill = white] {$= 1$}; \draw (f.north) -- ($(2sc.south west)!(f.north)!(2sc.south east)$) node [midway, right, font = \footnotesize\itshape] {Beweis auf S. 42}; \end{tikzpicture}
Wir beginnen eine neue Seite.
\clearpageAuf dieser Seite soll es ein {tikzpicture} geben, dass keinen eigenen Platz beansprucht, weshalb wir wieder overlay angeben. Die Option remember picture ermöglicht es uns nicht nur auf von uns benannte Nodes zuzugreifen, sondern auch auf den von TikZ definierten Seiten-Node mit dem Namen current page.
Wir legen außerdem fest, dass alle Nodes rot, fett, größer und kursiv sein sollen.
\begin{tikzpicture}[ remember picture, overlay, every node/.style = { red, font = \itshape\large\bfseries, } ]
Dann zeichnen wir fünf Nodes, deren Position wir jeweils auf einen Anker des current page-Node beziehen.
\node (OL) at ($(current page.north west)+(1,-1)$) [rotate = 45] {In}; \node (OR) at ($(current page.north east)+(-1,-1)$) [rotate = -45] {allen}; \node (UR) at ($(current page.south east)+(-1,1)$) [rotate = 225] {vier}; \node (UL) at ($(current page.south west)+(1,1)$) [rotate = 135] {Ecken}; \node (C) at (current page.center) [align = center] {soll Liebe\\drin stecken};
Zuletzt verbinden wir diese Nodes noch mit einer roten Linie.
\draw [ultra thick, red] (OL) -- (OR) -- (UR) -- (UL) |- (C);
\end{document}Türchen 23 – Funktionen zeichnen
\begin{tikzpicture}[thick]Als erstes zeichnen wir die Achsen des Koordinatensystems.
\draw [->] (-0.5,0) -- (8.5,0) node [below] {$x$}; \draw [->] (0,-2.5) -- (0,2.5) node [right] {$y$};
Dann benutzen wir die plot-Operation gemeinsam mit coordinates, um eine einfache Liste von Koordinaten auszugeben.
\draw [blue] plot coordinates {(0,0) (2,2) (4,0) (6,-2) (8,0)};
Mit der Option smooth, können wir den Graphen etwas glätten.
\draw [blue] plot coordinates {(0,0) (2,2) (4,0) (6,-2) (8,0)};
Wir können die nötigen Koordinaten auch von TikZ berechnen lassen. Dazu müssen wir die gewünschte Funktion als eine Koordinate angeben, wobei \x die Variable ist. Das r im Sinus sorgt für eine Interpretation im Bogenmaß. Den Wertebereich geben wir mit der Option domain an.
\draw [teal] plot [domain = 0:8] (\x, {2*sin(\x r)}) ;
Allerdings ist die Funktion etwas eckig geraten, anstatt mit smooth Abhilfe zu schaffen, erhöhen wir dieses Mal mit samples die Anzahl der Datenpunkte.
\draw [teal, dotted] plot [samples = 100, domain = 0:8] (\x, {2*cos(\x r)}) ;
Für komplexere Funktionen kann TikZ die Arbeit auch von GNUPLOT übernehmen lassen. Dazu muss auf dem Computer GNUPLOT installiert sein und Shell-Escape aktiviert werden (FAQ 16). TikZ legt dann eine Datei mit der Endung .gnuplot an, die mit GNUPLOT zu einer Datei mit der Endung .table verarbeitet wird, die wiederum von TikZ eingelesen wird.
Um eine Funktion mit GNUPLOT zu zeichnen, verwenden wir function gefolgt von der Funktion in GNUPLOT-Syntax. Über die Option id können wir jedem Graphen einen (im ganzen Dokument) eindeutigen Namen geben. Dadurch kann TikZ beim nächsten Kompilieren auf bereits erstellte .table-Dateien zurück greifen, was Rechenleistung und damit Zeit spart.
\draw [green!50!black] plot [id = plot1, samples = 500, domain = 0:8] function {2*exp(-x)*sin(8*x)};
\end{tikzpicture}Die weiteren Möglichkeiten von plot sind in Abschnitt 22 dokumentiert. Außerdem sei an dieser Stelle noch das sehr praktische Paket pgfplots erwähnt.
Türchen 24 – Zusammenfassung: Ein Weihnachtsbaum
Für eine „festliche“ Schrift laden wir das Paket chancery, das wir im LaTeX Font Catalogue gefunden haben.
\usepackage{chancery}
Außerdem laden wir für den Tannenbaum verschiedene Bibliotheken, die wir aus dem Kalender bereits kennen.
\usetikzlibrary{ arrows.meta, backgrounds, calc, decorations.pathmorphing, decorations.text, shapes.geometric, }
\begin{tikzpicture}[Um unseren Baum mit Kugel schmücken zu können, definieren wir diese als Pic.
kugel/.pic = { \shade [ball color = yellow!60!brown] (0,-0.9) circle [radius = 0.3]; \draw [ ultra thick, red, -{>[scale=0.6]<[scale=0.9]}, ] (0,-0.6) -- (0,0); \shade [ left color = yellow!40!brown, right color = yellow!30!black, ] (-0.1,-0.62) to[bend right, looseness = 0.6] (0.1,-0.62) -- ++(0,0.1) -| cycle; },
Ende der Optionen von {tikzpicture}
]
Als erstes zeichnen wir einen Stern als Node mit star-Form und benennen diesen als Stern.
\node (Stern) [ star, star point height = 6mm, minimum size = 20mm, thick, draw = yellow!60!brown, inner color = yellow!40!brown, outer color = yellow!80!brown, rotate = 50, ] at (3,14) {};
Um einen Schweif zu ergänzen, benutzen wir ein {scope}, das wir auf die Hintergrundebene legen. Auf diese Weise können wir den Schweif auf den Stern-Node beziehen und gleichzeitig dahinter platzieren.
\begin{scope}[on background layer] \shade [ left color = yellow!60!brown, right color = white, ] ($(Stern.center)-(0,0.1)$) -- ($(Stern.center)+(0,0.1)$) to[bend left] ++(4,1) -- ++(0.5,-1.5) to[bend right] cycle; \end{scope}
Den Stamm zeichnen wir ebenfalls in einem {scope}, um die Auswirkungen von \clip zu begrenzen. Für ein Rindenmuster benutzen wir eine \foreach-Schleife in Kombination mit der random steps-Dekoration.
\begin{scope} \filldraw [ fill = brown!55!black, draw = brown!35!black, thick, ] (-1,0) rectangle (1,2); \clip (-1,0) rectangle (1,2); \foreach \x in {-1,-0.9,...,1} \draw [ brown!35!black, ultra thick, decoration = { random steps, segment length = 1mm, amplitude = 0.25mm }, decorate ] (\x,0) -- ++(0,2); \end{scope}
Die Äste zeichnen wir mit einer \foreach-Schleife, die zwei Variablen (\b: Breite, \y: vertikale Position) hat, und deren Wiederholungen als \n mitgezählt werden. Während des Zeichnens ergänzen wir auf dem Pfad verschiedene Koordinaten, an denen wir später die Dekoration „befestigen“ wollen.
In der Beispiel-Datei findet sich am Ende eine weitere Schleife, um die Koordinaten sichtbar zu machen.
\foreach \b/\y [count = \n] in {6/2, 5.5/3.5, 5/5, 4.5/6.5, 3.5/8, 2.5/9.5} \shadedraw [ outer color = green!35!black, inner color = green!60!black, draw = green!35!black, looseness = 0.6, ] (-\b,\y-0.5) coordinate (L-\n) to [bend right] coordinate [midway] (LM-\n) (0,\y) coordinate (M-\n) to [bend right] coordinate [midway] (RM-\n) (\b,\y-0.6) coordinate (R-\n) to [bend left] coordinate [pos = 0.2 + 0.05*rand] (RS-\n) (0,\y+4) coordinate (S-\n) to [bend left] coordinate [pos = 0.8 + 0.05*rand] (LS-\n) cycle;
Die Spitze setzen wir aus einer Fläche und einer Linie mit verschiedenen Pfeilspitzen zusammen.
\shadedraw [ left color = yellow!20!brown, right color = yellow!80!brown, draw = yellow!40!brown, looseness = 0.4, ] ($(S-6)-(0.45,1.5)$) to [bend right] ++(0.9,0) to [bend left] ($(S-6)+(0,0.25)$) to [bend left] cycle; \draw [ draw = yellow!40!brown, ultra thick, >>-{Rays[n = 6, width = 4mm, length = 4mm]}, line cap = round, ] ($(S-6)+(0,-0.4)$) -- ++(0,0.8);
Für die Girlanden benutzen wir jetzt die beim Zeichnen der Äste definierten Koordinaten. Um die Einstellungen für zwei \draw-Pfade gleichzeitig zu machen, verwenden wir ein {scope}.
\begin{scope}[ ultra thick, decoration = { coil, aspect = 0.4, amplitude = 2mm, segment length = 1.5mm, }, ] \draw [red, decorate, bend right] (LS-6) to (RS-5) (LS-4) to (RS-3) (LS-2) to (RS-1); \draw [red!75!black, decorate, bend left] (RS-6) to (LS-5) (RS-4) to (LS-3) (RS-2) to (LS-1); \end{scope}
Nun „hängen“ wir noch die Kugeln an den Baum, die wir oben bereits als Pic definiert haben.
\path ($(S-6)-(0.3,2.75)$) pic {kugel} ($(S-4)-(1.1,3.15)$) pic {kugel} ($(S-4)+(1.2,-3.4)$) pic {kugel} ($(S-2)-(1.9,3.8)$) pic {kugel} ($(S-2)+(0.2,-3.3)$) pic {kugel} ($(S-2)+(1.8,-3.6)$) pic {kugel};
Zuletzt fügen wir noch gute Wünsche hinzu: Den ersten Text setzen wir als Pfad-Dekoration, wobei wir Text-Befehle wie \Huge in senkrechten Strichen | setzen müssen, damit TikZ diese verarbeiten kann. Den zweiten Text platzieren wir schlicht als Node.
\path [ decoration = { text along path, text = {|\Huge|Frohe Weihnachten!}, text align = left, }, decorate, ] (-5,13.5) to[bend left] ++(7,2); \node [ font = \Huge, ] at (4.5,-1.5) {… und einen guten Rutsch!};
\end{tikzpicture}Und nun?
Nun wünsche ich allen Lesern besinnliche, fröhliche und gerne auch mal computerfreie Weihnachtstage, eine erholsame Zeit zwischen den Jahren und einen guten Rutsch in das neue Jahr!
Das nächste Beispiel gibt es dann im Januar 2016 und wie immer gilt: Änderungen, Wünsche, Kritik und so weiter können Sie mir gerne über das Kontaktformular, per E-Mail oder via Twitter zukommen lassen.
Wer sich gerne weiter mit TikZ beschäftigen möchte, dem sei zu guter Letzt noch einmal die hervorragende Anleitung ans Herz gelegt. Viele Beispiele für die Mächtigkeit von PGF und TikZ sammelt die Seite TeXample.net.
Dieses Mal verwenden wir die Klasse
standalone, die das Seitenformat automatisch an eine (oder mehrere) Abbildungsgröße(n) anpasst. Dabei geben wir an, dass um die Abbildung(en) ein weißer Rand von 5 mm bleiben soll und durch die Optiontikzstellen wir ein, dass für jede{tikzpicture}-Umgebung automatisch eine eigene Seite angelegt wird.